| Прыгунов А.И.
проф., докт. техн. наук, зав кафедрой технической механики
Мурманского государственного технического университета
alexander.prygunov@mstu.edu.ru
Традиционные методы анализа физически реализованных сигналов, образов и временных рядов, порождаемых сложными (полимодальными) динамическими системами, в основном базируются на статистических методах, чаще всего на спектрально-корреляционных методах в различных их вариантах [1,2,3,4]. При этом, вследствие статистического подхода к анализу сигналов динамическая сущность процессов их порождающих, как правило, уходит на второй план. Современная нелинейная динамика позволяет рассмотреть анализ сигналов как процесс идентификации динамических систем по результатам анализа экспериментальных данных [5,6].
Если рассмотреть динамическую систему в виде системы дифференциальных уравнений вида L y(t) = f(t), где L - линейный дифференциальный оператор, становится очевидным, что физически реализуемыми решениями этой системы могут быть либо периодические моды, либо апериодические экспоненты, так как только эти функции порождают себе подобные производные. В том и другом случае могут порождаться как устойчивые, так и неустойчивые решения. В случае характерных динамических решений типа периодических мод речь следует вести преимущественно о структурной устойчивости, проявляющейся в локальной устойчивости к малым возмущениям топологической структуры фазовой траектории, соответствующей решению. В случае характерных для кинетики апериодических решений преимущественно следует говорить об устойчивости по Ляпунову. При этом, в глобальном плане неустойчивости соответствует режим инфинитного разбегания фазовой траектории решения, физически соответствующий разрушению системы (например, кинетика взрыва), а устойчивости постепенное затухание движений. Известно, что основным параметром, определяющим вариант решения, является вязкость (сопротивление) в системе. Обычно, апериодические решения кинетического типа характерны для систем с высоким демпфированием и характеризуют процессы относительно медленного развития.
В любом случае первоначальным этапом для исследования сигналов методами нелинейной динамики должна быть процедура реконструкции фазового траектории динамической системы, порождающей сигнал. Единственным методом, позволяющим реконструировать характер фазовой траектории системы на основе анализа экспериментально полученного сигнала, является процедура вложения (embedding procedure).
Основанием для такого подхода является теорема Такенса [5], которая утверждает, что путём правильного подбора размерности m и параметра задержки τ можно получить (m+1)-мерный фазовый образ достаточно полно отражающий свойства истиной траектории динамической системы в фазовом пространстве. Уравнение этой синтетической траектории может быть записано в виде zi+1 = x (t - iτ), где индекс (i+1) суть номер координаты реконструированного фазового пространства Z = {z1,...,zi+1}, а параметр i принимает целочисленные значения от 0 до m. В экспериментальных исследованиях динамики данная процедура называется вложением кратности m, а проекции получаемого (m+1)-мерного фазового образа {z1,...,zi+1} на плоскость {zj,zk}, где j<>k могут принимать значения от 1 до i+1, картами задержки. Утверждается, что размерность сложных процессов обычно находится в пределах от m=3 до m=6. Таким образом, размерность соответствующих фазовых образов от 4 до 7.
При проведении процедуры вложения важным параметром является задержка τ, которая не обязательно должна быть равна интервалу дискретизации h при цифровом анализе. Чаще всего её выбирают, исходя из ожидаемого или оценённого, например, по методу авторегрессии, периода одной из главных мод процесса. В последнем случае за период принимают временной интервал, соответствующий первому пересечению кривой авторегрессии с осью абсцисс.
Для машин роторного типа характерны гармонические сигналы вибрации с доминированием в спектре основной гармоники на частоте вращения. Поэтому для реконструкции соответствующей фазовой траектории обычно бывает достаточно получить трёхмерный образ {z1,z2,z3}. При этом наилучшее раскрытие траектории в проекции {z1,z2}, наблюдается при значениях задержки близких к четверти периода вращения. В тоже время, при таком выборе задержки в проекции {z1,z3} фазовый образ может выродиться в максимально компактную линию. В некотором смысле анализ карт задержки может рассматриваться как разновидность частотного анализа исходного сигнала. Наличие подобным образом вырожденных проекций является индикатором наличия выраженной гармоники в исходном сигнале. Рассмотрим примеры применения метода карт задержки к анализу вибрации машин роторного типа.
На рис.1а приведена типичная карта задержки для вертикальной вибрации машин роторного типа малой мощности с горизонтально расположенным ротором. Для этих машин характерна полная выборка зазора в подшипнике под влиянием только сил инерции от дисбаланса. На участие 1-2 цапфа находится в нижнем положении, и реакция направлена вверх, участок 2-3 соответствует выборке зазора и переходу цапфы в верхнее положение, на участке 3-4 цапфа находится в верхнем положении и реакция направлена вниз, участок 4-1 соответствует выборке зазора и переходу цапфы в нижнее положение. Точки возврата 1, 2, 3, 4 характеризуют динамику взаимодействия цапфы с подшипником в фазовые моменты начала и окончания выборки зазора. Для сравнения на рис. 1б приведена карта задержки для аналогичного подшипника, имеющего увеличенный зазор в посадочном месте наружного кольца в подшипниковом щите. В этом случае полной выборки зазора за счет действия только сил инерции не происходит (участок 3-4 отсутствует).

Рис. 1а |
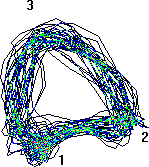
Рис. 1б |
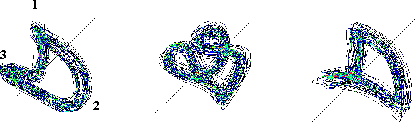
Рис. 2а, 2б, 2в На рис.2а приведена типичная карта задержки для вертикальной вибрации мощной машины роторного типа с горизонтально расположенным на подшипниках скольжения ротором. Для этих машин полная выборка зазора в подшипнике под влиянием только сил инерции от дисбаланса не характерна. Максимальному значению реакции опоры на ротор соответствует точка 1 на участке 1-2 реакция постепенно уменьшается, достигая минимальных значений на участке 2-3, на участке 3-1 происходит динамичное увеличение реакции (мягкий удар), начинающееся мягкой точкой возврата 3, соответствующей незначительному локальному увеличению трения. при неблагоприятном сочетании действующих в подшипнике сил. При этом, как правило, цапфа не выходит из контакта с нижней частью вкладыша и выборки зазора не происходит. Участок 1-3 характеризует динамику взаимодействия цапфы и вкладыша подшипника. Рост трения между цапфой и вкладышем подшипника проявляется в большем изгибе (деформации) участка 3-1 карты задержки (рис.2б). Карта рис.2в соответствует низкому трению но достаточно жёсткому ударному взаимодействию цапфы и вкладыша.
Из рассмотренных примеров видно, что карты задержки могут быть весьма удобными, информативными и высокочувствительными образами, характеризующими низкочастотную динамику подшипников машин роторного типа, в основном определяющую степень их вибронагруженности и остаточный ресурс.
Следует отметить, что карты задержки весьма чувствительны к малым изменениям частотного состава сигнала. В свою очередь, частотный состав сигнала характеризует совершенство формы волны процесса, соответствие её форме идеальной синусоиды. Достаточно вспомнить широко используемое в практической электротехнике понятие о коэффициенте нелинейных искажений в сети. Поэтому на основе анализа плоских проекций фазовых траекторий возможно получение высокочувствительных относительных количественных мер, характеризующих фазово-локальную форму сигнала.
Важной особенностью поведения сложных динамических систем является существенная нестационарность вплоть до хаотичности порождаемых ими сигналов. Поэтому прямое применение метода карт задержки к анализу сигналов такого типа невозможно. Как правило, требуется предварительная обработка сигнала по типу цифровой фильтрации для снижения числа значимых для построения карты задержки мод.
Традиционный спектральный анализ на базе быстрого преобразования Фурье (БПФ) не эффективен для нестационарных сигналов с временным масштабом нестационарности много меньшим продолжительности подлежащей анализу реализации. Это связано с усреднением мощности флуктуаций при спектральном анализе (спектр мощности) по всему времени наблюдения сигнала. Наиболее очевидным путём применения БПФ к анализу нестационарных сигналов является разбиение реализации на отдельные короткие равно длинные участки с последующим применением алгоритма БПФ к каждому из них. Этот приём широко известен в практике анализа сигналов как БПФ на коротких реализациях (Short Time Fast Fourier Transform или STFFT).
Математическим основанием для подобного подхода к анализу сигналов является широко известный метод решения линейных уравнений динамики, известный как метод функций Грина, заключающийся в решении уравнений для физически реализуемых динамических систем в виде свёртки
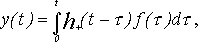 ,где h+ (t - τ) есть частный случай функции Грина и представляет собой нормальную реакцию системы на единичный импульс: Lh+(t-τ)=σ+(t-τ). Метод функций Грина представляет собой наиболее адекватный эксперименту метод решения дифференциальных уравнений, так как сводит процедуру их решения к свёртке произвольного внешнего воздействия на систему на импульсный отклик. Довольно часто в экспериментальных исследованиях идентификация динамических систем бывает связана с необходимостью тестового, например, импульсного воздействия на систему. Ясно, что алгоритм STFFT в обобщённом понимании может рассматриваться как отражение метода функций Грина применительно к анализу сигналов, так как он, по сути, основан на расчёте локальной свёртки сигнала на гармонику определённой частоты, которая при небольшом демпфировании в системе может рассматриваться как вариант отклика периодического типа на импульсное воздействие. ,где h+ (t - τ) есть частный случай функции Грина и представляет собой нормальную реакцию системы на единичный импульс: Lh+(t-τ)=σ+(t-τ). Метод функций Грина представляет собой наиболее адекватный эксперименту метод решения дифференциальных уравнений, так как сводит процедуру их решения к свёртке произвольного внешнего воздействия на систему на импульсный отклик. Довольно часто в экспериментальных исследованиях идентификация динамических систем бывает связана с необходимостью тестового, например, импульсного воздействия на систему. Ясно, что алгоритм STFFT в обобщённом понимании может рассматриваться как отражение метода функций Грина применительно к анализу сигналов, так как он, по сути, основан на расчёте локальной свёртки сигнала на гармонику определённой частоты, которая при небольшом демпфировании в системе может рассматриваться как вариант отклика периодического типа на импульсное воздействие.
Отличительной особенностью анализа на коротких реализациях является необходимость применения сглаживающих окон. Как известно, без них усиливается влияние эффекта растекания дискретных составляющих в боковые лепестки. Кроме того, увеличение числа участков разбиения исходной реализации ограничивает разрешающую способность анализа во временной области, поэтому в настоящее время предложен ряд алгоритмов анализа со скользящими сглаживающими и взвешивающими (усредняющими) окнами.
Наиболее известными вариантами время-частотного анализа высокого разрешения являются наиболее ранний анализ со скользящим гауссовским окном (окно Габора) [7]и наиболее развитый и эффективный вариант анализа этого типа известный как распределение Вигнера-Вилли (WVD). [8]. Применение алгоритмов анализа со скользящими окнами позволяет существенно увеличить разрешающую способность анализа во временной области при сохранении достаточно высокого разрешения в частотной области, однако сопряжено со значительным увеличением объёма вычислений. Рассмотренные методы анализа широко применяются при углублённом анализе сигналов во время-частотной области, например при распознавании речи. В настоящее время показано [9], что декомпозиция сигнала под скользящими окнами является частным случаем декомпозиции сигнала (образа) в новом типе ортогонального базиса известного как базис всплесков (wavelet basis).
По своей сути базис всплесков представляет собой ортогональный базис разложения функций в функциональном гильбертовом пространстве, элементы которого определяются параметрами a, b и задаются выражением
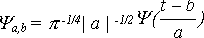 (1)где Ψ(t) - производящая или материнская функция. (1)где Ψ(t) - производящая или материнская функция.
В качестве производящей функции можно использовать её основной вариант, известный как функция Морле, которую можно записать в виде:
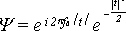 (2)где (2)где 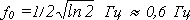 , t - время в с. Анализ функции (2) показывает, что она представляет собой гармонику с частотой f0 под окном , t - время в с. Анализ функции (2) показывает, что она представляет собой гармонику с частотой f0 под окном 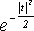 . Форма этого окна близка к форме окна Габора (гауссовский колокольчик). На рис.3 приведён качественный вид реальной части функции (2), который называют всплеском или вэйвлетом. . Форма этого окна близка к форме окна Габора (гауссовский колокольчик). На рис.3 приведён качественный вид реальной части функции (2), который называют всплеском или вэйвлетом.
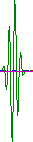
Рис. 3 Следует отметить, что выбор значения f0 задаёт соотношение между эффективной шириной окна и периодом анализируемой гармоники. В нашем случае эффективная ширина окна во временной области принята равной периоду анализируемой гармоники, что соответствует максимальной разрешающей способности анализа по времени.
Если принять значение параметра шкалы a = 2-j/B и параметра временной локализации b = 2-j/B k, где j, k - натуральные числа; B - число полос анализа приходящихся на октаву, то выражение для коэффициентов декомпозиции сигнала x(t) в базисе Ψa,b(Ψjk)примет вид:
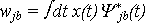 (3)где (3)где
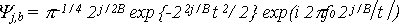 (4)B - число полос, приходящихся на одну октаву; t - время, которое для сигналов в цифровой форме может быть получено в виде t=h(n-b), где h - интервал дискретизации; n и b - целые числа, соответствующие текущему отсчёту и номеру отсчёта, соответствующему максимуму всплеска, соответственно. Звездочка означает процедуру комплексного сопряжения. (4)B - число полос, приходящихся на одну октаву; t - время, которое для сигналов в цифровой форме может быть получено в виде t=h(n-b), где h - интервал дискретизации; n и b - целые числа, соответствующие текущему отсчёту и номеру отсчёта, соответствующему максимуму всплеска, соответственно. Звездочка означает процедуру комплексного сопряжения.
Отличительной особенностью анализа в базисе всплесков является его высокая чувствительность к кратковременным высокочастотным флуктуациям сигнала, так как окно всплеска обеспечивает адекватную оценку таких флуктуаций за счёт одновременного увеличения амплитуды окна при уменьшении его ширины. Следует отметить, что в связи с анализом в базисе всплесков часто упоминают принцип неопределённости Гейзенберга. Разрешающая способность анализа во временной области возрастает с ростом частоты. В этом заключается принципиальное отличие анализа в базисе всплесков от преобразования Фурье на коротких реализациях, при котором разрешающая способность анализа по времени не зависит от частоты и связана только с разрешающей способностью анализа в частотной области.
Опыт работы с преобразованием (3), (4) привёл к выводу о том, что в большинстве случаев для оценки эволюции мод во времени достаточно проведения анализа для основной и трёх высших гармоник анализируемой моды. Это достигается при уже при 1/3-октавном анализе в базисе всплесков. Номер треть-октавной полосы, соответствующей основной гармонике колебания найдём из соотношения
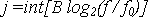 (5) (5)
Для фиксированного значения b коэффициенты разложения для основной гармоники wj1,b и трёх высших гармоник wj2,b, wj3,b, wj4,b могут быть найдены из выражения (3) при j1 = int{B[log2 (f/f0)]}≈ int[3(log2 f)+2,2]; j2= j1+3; j3= j1+5; j4= j1+6, где f - частота основной гармоники. На рис.4 приведен базис разложения сигнала по всплескам, мерой корреляции сигнала, с которым в текущий момент времени являются коэффициенты wjl,b.
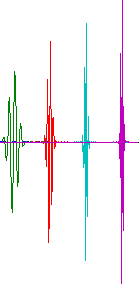
Рис. 4 Эффективность анализа с использованием разложения по базису всплесков можно проиллюстрировать на примере анализа вибрации среднеоборотного судового дизеля.
Поршневые машины характеризуются фазово детермированной динамикой, поэтому анализ их вибрации наиболее целесообразно проводить во время-частотной области с фазовым селектированием. На рис.5 приведены результаты анализа в базисе всплесков виброускорения цилиндровой втулки крупного судового дизеля (6ЧРН 52,5/72).
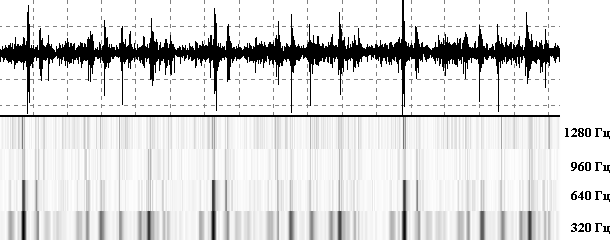
Рис. 5 Собственная частота колебаний втулки 320 Гц, поэтому анализ проведён именно для этой частоты. Собственная частота возбуждена на достаточно коротких фазовых интервалах, что является хорошей иллюстрацией необходимости повышения разрешающей способности анализа во времени в ряде практических приложений. В моменты вспышки уровни высших гармоник так же высоки, что свидетельствует о существенном отклонении формы колебаний в этот фазовый момент от синусоиды собственной частоты. Однако, в области низких цилиндровых давлений имеется ряд импульсов малой амплитуды близких к чистому тону на частоте 320 Гц, что приводит к выводу о возможности разработки на базе время-частотного анализа принципиально нового метода анализа, основанного не на амплитудно-частотном анализе, а на поиске в сигнале моментов возбуждения чистых мод совершенной тональной формы, с целью оценки с высоким разрешением эволюции во времени не только амплитуды, но и формы сигнала.
Большинство сигналов, генерируемых сложными динамическими системами, являются полимодальными сигналами, поэтому их динамический анализ базируется на разработке процедур позволяющих снижать модальность сложного сигнала путём выделения наиболее существенных мод, число которых определяет динамическую размерность процесса.
Для перехода от результатов время-частотного анализа во время-фазовую область по типу карт задержки можно синтезировать образ текущей фазовой траектории так же с помощью процедуры вложения, но с известными априори параметрами τ и m. Первым шагом на основе четырёх известных текущих коэффициентов разложения сигнала в базисе всплесков генерируется текущая четырёхмодальная модель сигнала
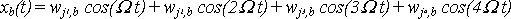 (6)для которой при каждом фиксированном b строится соответствующая фазовая траектория при τ = 0,5(π/Ω). Дальнейшему анализу подвергается проекция {z1,z2}, исходя из того, что в случае совершенной локальной формы сигнала (синусоида с основной частотой время-частотного анализа) эта проекция должна быть окружностью на периоде T=2π/Ω. Мерой сходства формы сигнала с совершенной формой предложено считать отношение площади A, заметаемой радиусом вектором точки на фазовой траектории в проекции {z1,z2} за период Т, к площади круга с диаметром D (6)для которой при каждом фиксированном b строится соответствующая фазовая траектория при τ = 0,5(π/Ω). Дальнейшему анализу подвергается проекция {z1,z2}, исходя из того, что в случае совершенной локальной формы сигнала (синусоида с основной частотой время-частотного анализа) эта проекция должна быть окружностью на периоде T=2π/Ω. Мерой сходства формы сигнала с совершенной формой предложено считать отношение площади A, заметаемой радиусом вектором точки на фазовой траектории в проекции {z1,z2} за период Т, к площади круга с диаметром D
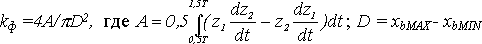 (7)Эту безразмерную относительную меру kф предложено называть коэффициентом формы сигнала. Следует отметить, что текущее значение коэффициента формы может быть рассчитано для каждого b. Таким образом, мы получаем отображение исходного сигнала в область, которую можно назвать областью "форма-время" и обозначить как {kф (b)} или {kф(t)}. Соответствующие кривые можно условно назвать формограммами. Если провести расчёт коэффициента формы для широкого диапазона частот (периодов) в каждой позиции окна b, то можно сформировать трёхмерные образы "время-частота-форма" {kф (t,f)} и "время-период-форма" {kф (t,T)} по типу традиционного при время-частотном анализе отображения "время-частота-спектральная мощность" {Pf (t,f)}. В практических приложениях наиболее удобно использовать отображение "время-период-форма". Такие образы условимся называть спектрограммами формы (Form Index Maps). Рассмотрим применение анализа на ряде простейших примеров. (7)Эту безразмерную относительную меру kф предложено называть коэффициентом формы сигнала. Следует отметить, что текущее значение коэффициента формы может быть рассчитано для каждого b. Таким образом, мы получаем отображение исходного сигнала в область, которую можно назвать областью "форма-время" и обозначить как {kф (b)} или {kф(t)}. Соответствующие кривые можно условно назвать формограммами. Если провести расчёт коэффициента формы для широкого диапазона частот (периодов) в каждой позиции окна b, то можно сформировать трёхмерные образы "время-частота-форма" {kф (t,f)} и "время-период-форма" {kф (t,T)} по типу традиционного при время-частотном анализе отображения "время-частота-спектральная мощность" {Pf (t,f)}. В практических приложениях наиболее удобно использовать отображение "время-период-форма". Такие образы условимся называть спектрограммами формы (Form Index Maps). Рассмотрим применение анализа на ряде простейших примеров.
На рис.6 представлены результаты анализа формы {kф (t,T)}|t=const для модельного сигнала, состоящего из одной гармоники с частотой 60 Гц (период 0,016 с).
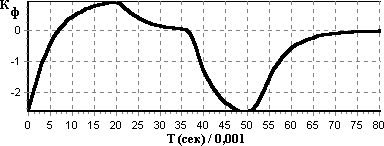
Рис. 6 Из рисунка видно, что на периоде, соответствующем основной частоте, коэффициент формы достигает максимального значения близкого к 1,0, на периоде в два раза большем обращается в ноль, вследствие вырождения соответствующей карты задержки в линию. На периоде в три раза большем основного коэффициент формы достигает своего минимального отрицательного значения близкого к (−3,0). Это связано с тем, что соответствующая карта задержки формируется путём троекратного вращения за основной период в направлении противоположном исходному направлению вращения. Как увидим в дальнейшем, это свойство коэффициента формы важно для фазовой локализации гармоник. Гармоника может быть локализована дважды: по наибольшему и наименьшему значениям коэффициента формы. При достижении периода в четыре раза большего основного коэффициент формы вновь стремится к нолю, вследствие вырождения соответствующей карты задержки.
На рис.7 представлена формограмма для ударно импульсного сигнала, полученного путём бросания твердого шарика на упругую подложку.
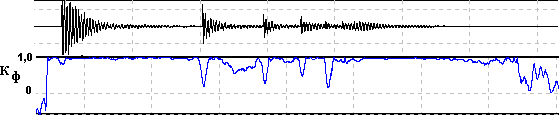
Рис. 7 Из рисунка становится понятной сущность метода. Видно, что значение коэффициента формы не зависит от амплитуды сигнала, так как, несмотря на уменьшение амплитуды колебаний подложки, форма колебаний остаётся в высокой степени гармонической. В тоже время импульсы от удара и подскоков генерируют характерный для импульсных сигналов полигармонический спектр, что приводит к локальному уменьшению коэффициента формы в основном за счёт возбуждения третьей гармоники собственной частоты. Отрицательное значение приобретаемое коэффициентом формы при наличии в сигнале третьей гармоники может быть выгодно при анализе. Все четыре импульса от отскоков в ходе анализа уверенно зафиксированы.
Коэффициент формы в рассматриваемом примере сохраняет своё максимальное значение при уменьшении амплитуды сигнала в процессе затухания вплоть до уровня шума. Уровень шума в эксперименте был примерно на 40 дБ ниже максимального уровня сигнала. Из примера видно существенное отличие предлагаемого метода анализа от традиционных амплитудно-частотных методов, заключающееся в том, что амплитуда (энергия) становится несущественной по сравнению с формой. Даже малому сигналу совершенной формы по результатам анализа соответствует максимальное значение коэффициента формы.
Это свойство анализа имеет фундаментальное значение, так как на его результаты практически не влияет амплитудный шум характерный для сигналов вибрации машин. В тоже время анализ не оставляет без внимания ни одной моды проявляющейся в сигнале вне зависимости от её амплитуды. Возможность реализации в ходе эксперимента модального анализа сложных нестационарных процессов открывает новые перспективы в исследованиях вибрации машин. Рассмотрим в этой связи практический пример.
Высокой нестационарностью отличаются вибрационные процессы в машинах с возвратно-поступательными кинематическими парами (двигатели внутреннего сгорания, поршневые насосы и компрессоры). На рис.8 представлена спектрограмма формы сигнала вибрации полученного с цилиндровой втулки судового среднеоборотного дизеля (виброускорение). В нижней части рисунка представлен характер виброграммы за один цикл работы цилиндра, в правой части представлена шкала изменения интенсивности затемнения рисунка в зависимости от значения коэффициента формы, которые принимают значения от 1,0 (тёмные области) до −3,0 (светлые области). Шкала периодов отградуирована в интервалах дискретизации сигнала, который в нашем случае был равен 400 мкс. Зонам локального потемнения, соответствующим собственной частоте втулки соответствует период 2,8 мс (7 единиц шкалы), о гармоническом характере колебаний свидетельствует наличие соответствующих зон локального просветления на периоде в три раза большем (21 единица шкалы). Нестационарный характер сигнала проявляется в том, что области потемнения и просветления локализованы по фазе работы цилиндра. Имеются три разрыва области генерации основной формы: в областях близких к нижним мёртвым точкам (окончание расширения и начало сжатия) и верхней мёртвой точки (ВМТ) компрессорного хода поршня.
С областями разрывов ассоциируются проявления субгармонической формы 1/2 (темные зоны на периоде 14 и светлые на периоде 42). В области разрыва после ВМТ компрессорного хода наблюдается проявление генерации гармоники близкой к субгармонике 1/3 (светлое пятно на периоде 70). Регистрация субгармонической генерации по амплитудам затруднена вследствие высоких энергетических затрат на их возбуждение и низкой разрешающей способности спектрального анализа со скользящим окном в области низких частот. В тоже время, генерация субгармоник является важным эффектом характерным для нелинейных неконсервативных систем и тесно связана с процессами диссипации механической энергии.
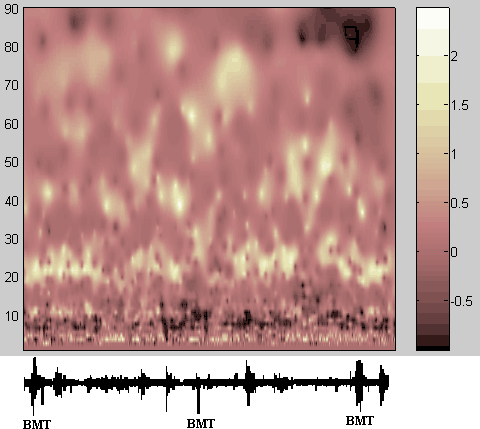
Рис. 8 В конце расширения и в начале сжатия наблюдаются наклонные цепочки светлых пятен, формирующие структуры типа "ласточкин хвост" для периодов от 30 до 55, что свидетельствует о явно нелинейном, в смысле зависимости собственных частот от параметров, поведении процесса в эти фазовые моменты.
Пример показывает высокую чувствительность анализа формы к изменению модального состава нестационарных процессов в машинах в целях выявления основных нелинейных эффектов, таких как генерация субгармоник, дрейф собственных частот и т.д.
Одной из причин усталостного разрушения зубчатых передач и подшипников, входящих в состав приводов механизмов газораспределения дизелей является нелинейный субгармонический резонанс, возникающий в зацеплении под влиянием импульсного характера нагрузки топливных насосов высокого давления (ТНВД). Для резонанса характерна выраженная анизотропия вибрации по направлениям и частота в два раза меньшая частоты зацепления. На рис.9 показаны результаты анализа формы колебаний на частоте резонанса, полученные на цапфе промежуточной шестерни привода ТНВД судового дизеля в радиальном и продольном направлениях.
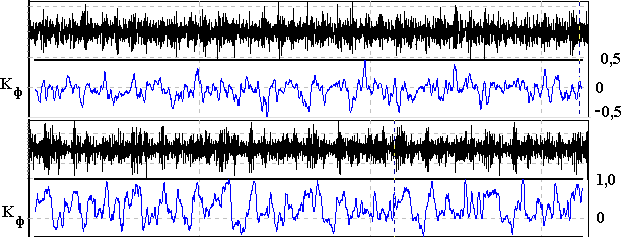
Рис. 9 Из рисунка видно, что среднее значение коэффициента формы для вертикального направления (верхняя формограмма) близко к нулю, в то время как среднее значение коэффициента формы для продольного направления (нижняя формограмма) составляет 0,53. Таким образом, из примера видно, что возникновение и развитие резонанса в области привода ТНВД может контролироваться и нормироваться, исходя только из расчёта среднего значения коэффициента формы, что удобно использовать при разработке автоматизированной системы диагностики данного вида дефектов. Детальное рассмотрение формограмм с учётом возможности фазовой привязки позволяет определить топливные насосы, на фазе работы которых наблюдается наибольшее развитие резонанса, что позволяет дать конкретные технологические рекомендации по устранению дефекта путём регулировки зазоров и биений в зацеплении на фазе работы соответствующих плунжеров.
По аналогии с предыдущим примером рассмотрим дополнительно спектрограмму формы для продольной вибрации, которая приведена на рис.10.
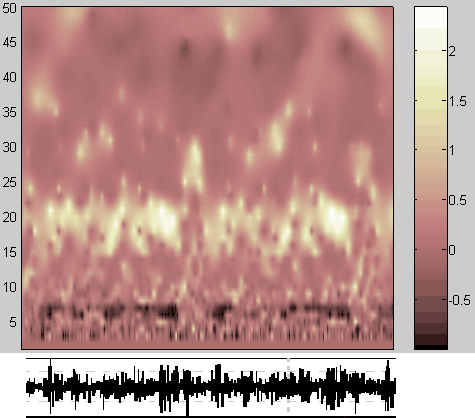
Рис. 10 Интервал дискретизации в данном случае составляет 1,6 мс, поэтому частоте нелинейного резонанса 90 Гц соответствует период 11 мс или 7 единиц шкалы. Нижней формограмме с рис.9 на рис.10 соответствует горизонтальное сечение спектрограммы формы на уровне 7 ед. шкалы, где и расположены основные её тёмные области. Светлые области на уровне 21 ед. шкалы подтверждают гармонический характер колебаний на частоте резонанса. Небольшой угловой наклон серий пятен соответствует незначительной зависимости частоты резонанса от параметров нагрузки, характерной для нелинейных резонансов. Обращает на себя внимание проявление один раз за цикл машины светлой области спекетрограммы на уровне 30 ед. шкалы при одновременном подавлении в эти моменты основной формы. Если зубцовая частота привода составляет 180 Гц, то третьей ее субгармонике соответствуют 60 Гц и гармонические колебания с этой частотой должны проявляться в виде светлого пятна на периоде 50 мс, чему соответствует 30 ед. шкалы. Таким образом, зафиксирован важный эффект, подтверждающий нелинейный характер резонанса в механизме привода ТНВД, в смысле высокой чувствительности к малым изменениям управляющих параметров (зазоры, биения, параметры демпфирования), следствием чего является возможность быстрых изменений частоты резонанса. Следует отметить что субгармонический резонанс 1/3 в результатах прямого измерения вибрации не проявился.
Таким образом, при исследованиях нелинейных колебаний в машинах, сопровождающихся значительной нестационарностью вибрационного процесса, наряду с использованием традиционных методов время-частотного анализа может быть рекомендовано дополнительное использование основанного на методе карт задержки анализа формы сигналов, особенно в субгармонической области.
В заключение следует отметить, что применение интегральных методов оценки нестационарных вибрационных процессов, таких как показатели Ляпунова и фрактальные размерности реконструированных фазовых траекторий, к успеху не приводят по причине их низкой чувствительности к малым изменениям характера движения, что особенно важно при решении задач диагностики зарождающихся дефектов.
|

